Data struct Binary Search Tree

Nama: Dea Claresta
Nim: 2301863736

In computer science, binary search trees (BST), sometimes called ordered or sorted binary trees, are a particular type of container: a data structure that stores "items" (such as numbers, names etc.) in memory. They allow fast lookup, addition and removal of items, and can be used to implement either dynamic sets of items, or lookup tables that allow finding an item by its key (e.g., finding the phone number of a person by name).

Binary search trees keep their keys in sorted order, so that lookup and other operations can use the principle of binary search: when looking for a key in a tree (or a place to insert a new key), they traverse the tree from root to leaf, making comparisons to keys stored in the nodes of the tree and deciding, on the basis of the comparison, to continue searching in the left or right subtrees. On average, this means that each comparison allows the operations to skip about half of the tree, so that each lookup, insertion or deletion takes time proportional to the logarithm of the number of items stored in the tree. This is much better than the linear time required to find items by key in an (unsorted) array, but slower than the corresponding operations on hash tables.

The properties that separates a binary search tree from a regular binary tree is

1. All nodes of left subtree are less than root node
2. All nodes of right subtree are more than root node
3. Both subtrees of each node are also BSTs i.e. they have the above two properties

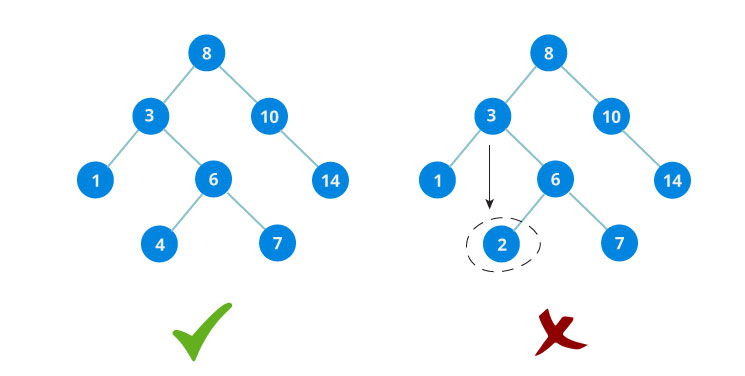
The binary tree on the right isn't a binary search tree because the right subtree of the node "3" contains a value smaller that it.

Creation of binary tree

Binary tree is created by inserting root node and its child nodes. We will use a C programming language for all the examples. Below is the code snippet for insert function. It will insert nodes.

11 void insert(node ** tree, int val) {
12 node *temp = NULL;
13 if(!(*tree)) {
14   temp = (node *)malloc(sizeof(node));
15   temp->left = temp->right = NULL;
16   temp->data = val;
17   *tree = temp;
18   return;
19 }
20
21 if(val < (*tree)->data) {
22      insert(&(*tree)->left, val);
23   } else if(val > (*tree)->data) {
24     insert(&(*tree)->right, val);
25   }
26 }

This function would determine the position as per value of node to be added and new node would be added into binary tree. Function is explained in steps below and code snippet lines are mapped to explanation steps given below.

[Lines 13-19] Check first if tree is empty, then insert node as root.

[Line 21] Check if node value to be inserted is lesser than root node value, then

• a. [Line 22] Call insert() function recursively while there is non-NULL left node
• b. [Lines 13-19] When reached to leftmost node as NULL, insert new node.

[Line 23] Check if node value to be inserted is greater than root node value, then

• a. [Line 24] Call insert() function recursively while there is non-NULL right node
• b. [Lines 13-19] When reached to rightmost node as NULL, insert new node.

Searching into binary tree

Searching is done as per value of node to be searched whether it is root node or it lies in left or right sub-tree. Below is the code snippet for search function. It will search node into binary tree.

46 node* search(node ** tree, int val) {
47 if(!(*tree)) {
48   return NULL;
49  }
50 if(val == (*tree)->data) {
51   return *tree;
52  } else if(val < (*tree)->data) {
53    search(&((*tree)->left), val);
54  } else if(val > (*tree)->data){
55    search(&((*tree)->right), val);
56  }
57 }

This search function would search for value of node whether node of same value already exists in binary tree or not. If it is found, then searched node is returned otherwise NULL (i.e. no node) is returned. Function is explained in steps below and code snippet lines are mapped to explanation steps given below.

1. [Lines 47-49] Check first if tree is empty, then return NULL.
2. [Lines 50-51] Check if node value to be searched is equal to root node value, then return node
3. [Lines 52-53] Check if node value to be searched is lesser than root node value, then call search() function recursively with left node
4. [Lines 54-55] Check if node value to be searched is greater than root node value, then call search() function recursively with right node
5. Repeat step 2, 3, 4 for each recursion call of this search function until node to be searched is found.

Deletion of binary tree

Binary tree is deleted by removing its child nodes and root node. Below is the code snippet for deletion of binary tree.

38 void deltree(node * tree) {
39 if (tree) {
40   deltree(tree->left);
41   deltree(tree->right);
42   free(tree);
43  }
44 }

This function would delete all nodes of binary tree in the manner – left node, right node and root node. Function is explained in steps below and code snippet lines are mapped to explanation steps given below.

[Line 39] Check first if root node is non-NULL, then

• a. [Line 40] Call deltree() function recursively while there is non-NULL left node
• b. [Line 41] Call deltree() function recursively while there is non-NULL right node
• c. [Line 42] Delete the node.

some of my materials were made by https://www.thegeekstuff.com/2013/02/c-binary-tree/

https://www.programiz.com/dsa/binary-search-tree

and https://en.wikipedia.org/wiki/Binary_search_tree.

thankyou to thegeeksstruff.com,wikipedia, and proramiz.com as my references of this blog:)