SEMUA RINGKASAN DATA STRUCTURE(Sebelum UTS-UAS)
Nama: Dea Claresta
Nim: 2301863736
Dosen Kelas Besar: Henry Chong (D4460),
Ferdinand Ariandy Luwinda (D4522),
Dosen Kelas Kecil: Diana (D4458).
Kelas: CB01-LB08
SEMUA RINGKASAN DATA STRUCTURE(Sebelum UTS-UAS)
Pointer
pointer digunakan untuk mengirimkan informasi diantar function.
pointer digunakan untuk mengirimkan array, string sebagai fungsi.
pointer biasanya digunakan untuk complex data structures, seperti linked list, trees, linked stacks, linked queues dan graphs.
Array
array adalah kumpulan data yg sama dalam satu elemen. dimana data-data ini memiliki type data yang sama.
Structure
structures merupakan tempat penyimpanan. structure dapat meyimpan data yang saling berhubungan walaupun memiliki data types yang berbeda-beda.structure memiliki keunggulan jika dibandingkan dengan array, dimana structure bisa menyimpan data sesuai dengan data yang ditambahkan. tidak seperti array yang jika ingin menyimpan data harus terlebih dahulu
Linked list
linked list adalah kumpulan linear dari elemen data dimana setiap elemen ini disebut nodes.
linked list dibagi menjadi dua yaitu single linked list dan double linked list.linked list ada 3 bagian, yaitu head, current, dan tail, dimana setelah tail selalu =NULL. Posisi head selalu berada di depan rantai , dan tail ada di paling belakang rantai. Current bisa berpindah
pindah ke posisi manapun.
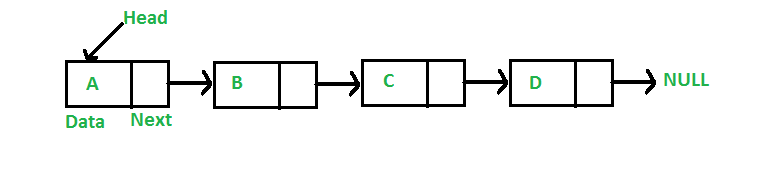
Single linked list
single linked list adalah tipe linked list yang paling simple dimana setiap node mengandung beberapa data dan pointer ke node selanjutnya dimana setiap nodes menyimpan alamat dari node selanjutnya . single linked list hanya bisa melalui data-data dalam satu jalur atau arah.
struct node
{
int data;
struct node *next; // Pointer to next node
};
Stacks
stack adalah data yang disimpan dalam baris yang terurut.Dalam linked list, mampu melakukan 3 operasi dalam stack, yaitu pop, push dan peek.
Pop
pop adalah operation yang menghapus sebuah element dari stack.
Push
Push merupakan operai yang menambahkan data dalam sebuah stack
Peek
Peek merukan operasi yang menunjukkan semua data dalam stack yang ada


Circular linked list
circular linked list sama seperti single linked list, namun, pada tail nya dia akan kembali lagi ke data paling depan, sehingga terbentuk seperti lingkaran data.
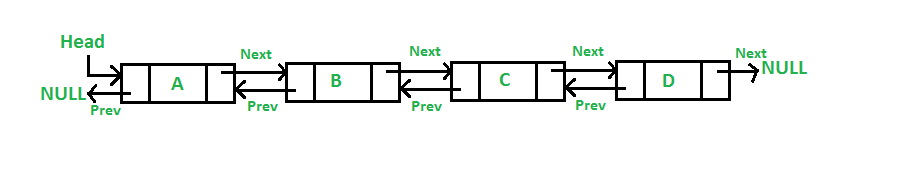
Double linked list
double linked list merupakan linked list yang memiliki dua arah sehingga memiliki 3 part data, yaitu data node, pointer ke previous dan pointer ke next .dalam double linked list, head->prev= NULL, dan tail>next=NULL
struct node
{
int data;
struct node *next; // Pointer to next node
struct node*prev;//pointer untuk node sebelumnya
struct node*prev;//pointer untuk node sebelumnya
};
Stacks
stack adalah data yang disimpan dalam baris yang terurut.Dalam linked list, mampu melakukan 3 operasi dalam stack, yaitu pop, push dan peek.
Pop
pop adalah operation yang menghapus sebuah element dari stack.
Push
Push merupakan operai yang menambahkan data dalam sebuah stack
Peek
Peek merukan operasi yang menunjukkan semua data dalam stack yang ada


Push depan,
Push depan adalah menyelipkan data di paling depan rantai data
Push depan adalah menyelipkan data di paling depan rantai data
Push belakang
push belakang adalah menambahkan data dari belakang rantai
push belakang adalah menambahkan data dari belakang rantai
Push
push biasa, dimana push ini menyelipkan data di antara data lainnya
push biasa, dimana push ini menyelipkan data di antara data lainnya
Pop depan,
pop depan adalah menghilangkan data paling depan
pop depan adalah menghilangkan data paling depan
Pop belakang
pop belakang adalah menghilangkan data di paling belakang
pop belakang adalah menghilangkan data di paling belakang
Pop
pop adalah menghapuskan data yang disebutkan
pop adalah menghapuskan data yang disebutkan
Pop all
pop all artinya menghapus semua data yang ada
Stacks
stack adalah data yang disimpan dalam baris yang terurut.Dalam linked list, mampu melakukan 3 operasi dalam stack, yaitu pop, push dan peek. stack sendiri memiliki prinsip masuk pertama, keluar terakhir ,seperti tumpukan piring
Pop
pop adalah operation yang menghapus sebuah element dari stack.
Push
Push merupakan operai yang menambahkan data dalam sebuah stack
Peek
Peek merukan operasi yang menunjukkan semua data dalam stack yang ada
Queue
berbeda dengan Stack , queue memiliki prinsip dimana masuk pertama , makan akan keluar pertama, seperti dalam antrian
Priority queue
Priority queue sama seperti queue namun ada beberapa hal yang diprioritaskan. jika dalam kehidupan nyata maka ini mirip dengan pasien di rumah sakit dimana pasien yang sudah tua dan gawat darurat akan selalu diutamakan.
Tree
tree merupakan hubungan dari node yang satu ke yang lainnya dimana akan ada satu node yang dianggap menjadi akar dan terus dipecah menjadi sub node -sub node lainnya
Hashing
hashing merupakan metode menyimpan data yang memiliki beragam cara
Binary tree
binary tree adalah data structures yang merupakan kumpulan elemen yang disebut node.Binary tree memiliki banyak macam, mulai dari complete binary tree, dan extended binary tree.
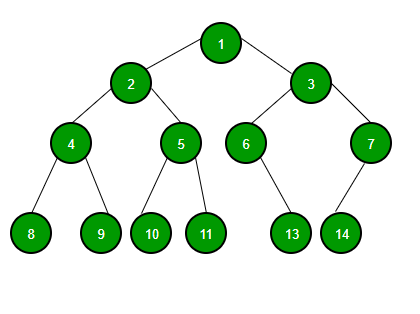
Binary search tree
binary search tree sama seperti ordered binary tree yang dimana merupakan varian dari binary tree dimana nodesnya tersusun rapi.
Gambar kedua untuk searching
gambar ketiga untuk delete
Dalam menghitung sebuah angka, komputer tidak bisa langsung membaca mana yan harus dilakukan dahulu , baik itu kali, pangkat, maupun tanda kurung. oleh sebab itu kita harus mengubah bentuk itu (infix) menjadi post fix dan prefix terlebih dahulu.
postfix: kiri,kanan ,print
prefix: print, kiri,kanan
infix:kiri ,print,kanan





pop all artinya menghapus semua data yang ada
Stacks
stack adalah data yang disimpan dalam baris yang terurut.Dalam linked list, mampu melakukan 3 operasi dalam stack, yaitu pop, push dan peek. stack sendiri memiliki prinsip masuk pertama, keluar terakhir ,seperti tumpukan piring
Pop
pop adalah operation yang menghapus sebuah element dari stack.
Push
Push merupakan operai yang menambahkan data dalam sebuah stack
Peek
Peek merukan operasi yang menunjukkan semua data dalam stack yang ada
Queue
berbeda dengan Stack , queue memiliki prinsip dimana masuk pertama , makan akan keluar pertama, seperti dalam antrian
Priority queue
Priority queue sama seperti queue namun ada beberapa hal yang diprioritaskan. jika dalam kehidupan nyata maka ini mirip dengan pasien di rumah sakit dimana pasien yang sudah tua dan gawat darurat akan selalu diutamakan.
Tree
tree merupakan hubungan dari node yang satu ke yang lainnya dimana akan ada satu node yang dianggap menjadi akar dan terus dipecah menjadi sub node -sub node lainnya
Hashing
hashing merupakan metode menyimpan data yang memiliki beragam cara
Binary tree
binary tree adalah data structures yang merupakan kumpulan elemen yang disebut node.Binary tree memiliki banyak macam, mulai dari complete binary tree, dan extended binary tree.

Binary search tree
binary search tree sama seperti ordered binary tree yang dimana merupakan varian dari binary tree dimana nodesnya tersusun rapi.
11 void insert(node ** tree, int val) {
12 node *temp = NULL;
13 if(!(*tree)) {
14 temp = (node *)malloc(sizeof(node));
15 temp->left = temp->right = NULL;
16 temp->data = val;
17 *tree = temp;
18 return;
19 }
20
21 if(val < (*tree)->data) {
22 insert(&(*tree)->left, val);
23 } else if(val > (*tree)->data) {
24 insert(&(*tree)->right, val);
25 }
26 }
6 node* search(node ** tree, int val) {
47 if(!(*tree)) {
48 return NULL;
49 }
50 if(val == (*tree)->data) {
51 return *tree;
52 } else if(val < (*tree)->data) {
53 search(&((*tree)->left), val);
54 } else if(val > (*tree)->data){
55 search(&((*tree)->right), val);
56 }
57 }
8 void deltree(node * tree) {
39 if (tree) {
40 deltree(tree->left);
41 deltree(tree->right);
42 free(tree);
43 }
Gambar kedua untuk searching
gambar ketiga untuk delete
Dalam menghitung sebuah angka, komputer tidak bisa langsung membaca mana yan harus dilakukan dahulu , baik itu kali, pangkat, maupun tanda kurung. oleh sebab itu kita harus mengubah bentuk itu (infix) menjadi post fix dan prefix terlebih dahulu.
postfix: kiri,kanan ,print
prefix: print, kiri,kanan
infix:kiri ,print,kanan
AVL Tree
Nama: Dea Claresta
Nim: 2301863736
AVL Tree merupalan self balancing binary search tree. BST digunakan dengan tujuan dari lebih cepatnya suatu node ditemukan, namun BST memiliki worst case, dimana proses penginputan data yg berurut akan membuat penempatan Node yang sebaris dan tidak bercabang,sehingga proses pencarian datanya sama saja dengan linked list yaitu dengan membandingkan setiap node dari awal sampai ketemu. Oleh sebab itu, digunakan lah metode AVL, yaitu balancingnya BST, sehingga setiap node hanya akan memiliki balence faktor maksimal 1 yang didapat dari pengurangan height kedua anaknya. Dimana setiap leaf(node yang tidak memiliki anak ) akan memiliki height sebesar satu, dan node-node keatasnya akan memiliki height yang semakin besar.
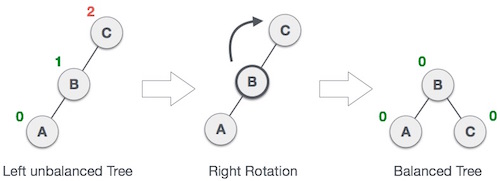
Jika setelah penginputan terbentuk balence factor yang lebih besar dari 1, maka akan dilakukan rotasi. Untuk rotasi ini sendiri, ada 4 macam( LL, RR, LR, RL). dimana rotasi ini dilihat dari 2 langkah terjadi imbalace menuju sumber terciptanya imbalance.
Delete node pada AVL
jika, node tidak memiliki anak, maka node tersebut akan dihapus, dan dilakukan pengecekan terjadi imbalance atau tidak, jika terjadi, maka dilakukan rotasi sesuai dengan cara diatas.
Jika node yang dihapus memiliki anak, maka digantikan oleh anak kiri paling kanan atau anak kanan paling kiri dari node tersebut. lalu dilakukan pengecekan ,terjadi imbalance atau tidak, jika terjadi maka melakukan rotasi sesuai dengan cara diatas.
Nim: 2301863736
AVL Tree merupalan self balancing binary search tree. BST digunakan dengan tujuan dari lebih cepatnya suatu node ditemukan, namun BST memiliki worst case, dimana proses penginputan data yg berurut akan membuat penempatan Node yang sebaris dan tidak bercabang,sehingga proses pencarian datanya sama saja dengan linked list yaitu dengan membandingkan setiap node dari awal sampai ketemu. Oleh sebab itu, digunakan lah metode AVL, yaitu balancingnya BST, sehingga setiap node hanya akan memiliki balence faktor maksimal 1 yang didapat dari pengurangan height kedua anaknya. Dimana setiap leaf(node yang tidak memiliki anak ) akan memiliki height sebesar satu, dan node-node keatasnya akan memiliki height yang semakin besar.
Jika setelah penginputan terbentuk balence factor yang lebih besar dari 1, maka akan dilakukan rotasi. Untuk rotasi ini sendiri, ada 4 macam( LL, RR, LR, RL). dimana rotasi ini dilihat dari 2 langkah terjadi imbalace menuju sumber terciptanya imbalance.
 |
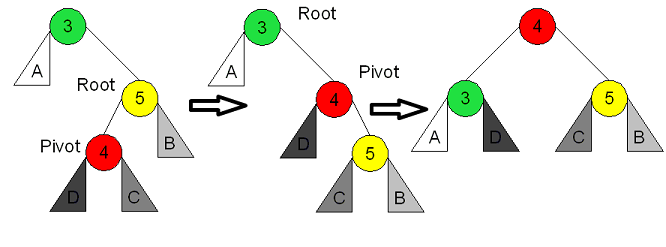
| Rotasi RR(right-right) pada node c terjadi imbalance, oleh sebab itu dilakukan rotasi, karena balace faktornya 2-0=2 ->lebih besar dr 1, karena 2 langkah menuju ke sumber imbalance adalah left-left, maka dilakukan rotasi RR, dan membuat node B menjadi parent, A&C menjadi anakn. jika node b memiliki anak kanan, maka anaknya akan tetap dikanannya, namun beradi di bawah node c(yang memberikan posisinya) |
 |
| Rotasi RL(right - left) imbalance terjadi di node 3, untuk menuju ke sumber imbalance, perlu ke kanan, lalu kiri, oleh sebab itu dilakukan rotasi RL,Rotasi RL adalah melakukan rotasi RR di node ke 5, dan rotasi LL di node 3 |
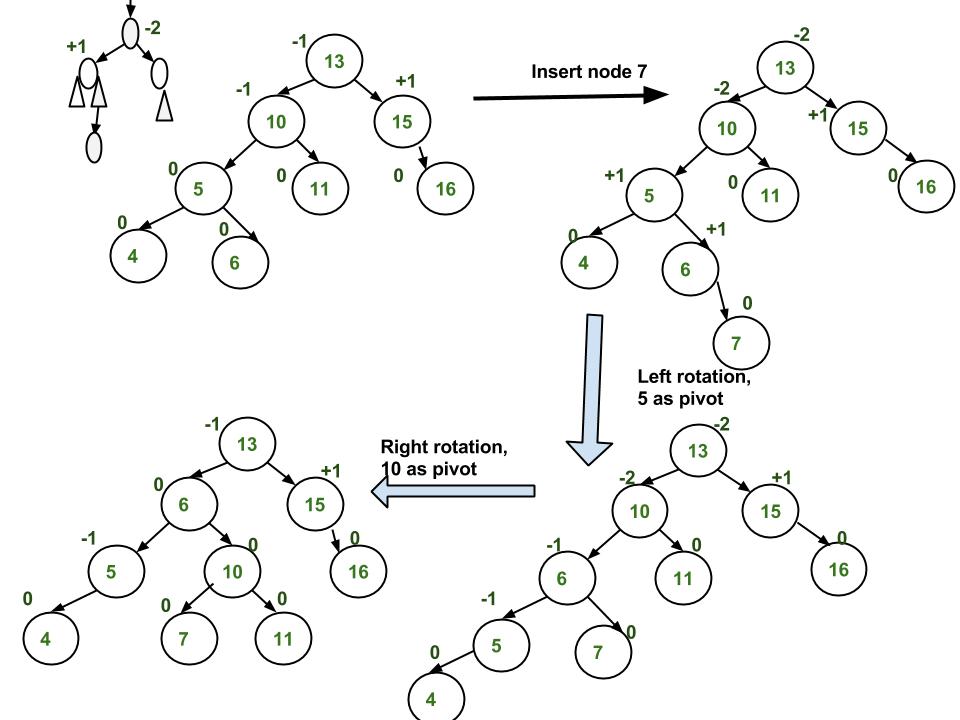 |
| Rotasi LR(left-right) setelah dimasukkan node 7, pada node 13 terjadi imbalance, karena balance faktornya 4-2=2-> lebih besar dari 1, namun, dibawahnya terdapat node yang juga imbalance, sehinggat yang dilakukan adalah node dibawahnya terlabih dahulu. node 10 juga imbalace . 2 langkah dari node 10 menuju node 7(penyebab imbalance) adalah kiri,kanansehingga dilakukan rotasi LR, sehingga pada node ke 5 dilakukan rotasi LL, lalu rotasi RR pada node 10, dan anak kanan 6 pindah ke anak kiri 10(yang turun) |
Delete node pada AVL
jika, node tidak memiliki anak, maka node tersebut akan dihapus, dan dilakukan pengecekan terjadi imbalance atau tidak, jika terjadi, maka dilakukan rotasi sesuai dengan cara diatas.
Jika node yang dihapus memiliki anak, maka digantikan oleh anak kiri paling kanan atau anak kanan paling kiri dari node tersebut. lalu dilakukan pengecekan ,terjadi imbalance atau tidak, jika terjadi maka melakukan rotasi sesuai dengan cara diatas.
Red Black Tree
Red Black Tree (RBT) adalah self balancing BST. Setiap node dalam RBT diwarnai dengan warna
hitam / merah. RBT membuat proses searching,insert, dan delete lebih cepat .
RBT memiliki proses yang mirip dengan BST, yaitu setiap node memiliki 2 anak,
jika node< dari parent, maka akan menjadi anak kiri, dan jika node>parent
maka akan menjadi anak kanan .

1. Insertion
-
New node selalu berwarna merah(Kecuali root,root
selalu hitam).
o
Jika
parentnya hitam, maka tidak terjadi violation.
o
Jika parentnya
merah, maka terjadi violation. Intinya, merah tidak boleh ketemu dengan merah.
-
External node(node kosong) selalu berwarna
hitam.
2. Violation
Jika terjadi violation, lihat
unclenya(parent’s sibling);
-
Jika unclenya merah, maka ubah parent dan uncle
jd black, dan grandparents jd red.
-
Jika unclenya black, maka melakukan single
rotasi (di grandparent) / duble rotasi(di parent lalu grandparent).
o
Lalu ubah yang sekarang parent jadi hitam, dan
anaknya jadi merah.
3. Deletion
Sama seperti BST, jika memiliki 2
anak, maka akan diganti dengan anak kiri paling besar/ anak kanan paling kecil.
Jika node yang dihapus adalah M dan penggantinya adalah C;
-
Jika M merah , maka di replace saja dengan C
-
Jika M hitam, dan C merah, maka replace dan
recolor C dengan hitam
-
Jika M & C hitam, replace M dengan C, lalu
anggap N lokasi baru C, P itu parentnya, S siblingnya, SL dan SR itu anaknya S ;
- Jika S merah, tukar warna N&P, rotate
di P
- Jika S,SL,&SR hitam maka recolor S
jadi Merah
- Jika S hitam dan SL&SR merah, maka
single/double rotate(di S)
Heap
Heap adalah spesial tree, yaitu complete binary tree. Heap ada 2 tipe, max heap, dan min heap.
Min heap->node parentnya lebih kecil dr anaknya. Max heap->parentnya lebih besar dari anaknya.
Min heap-> angka paling kecil ada di root. angka paling besarnya ada di salah satu leaf. heap bisa menggunakan linked list, tp paling mudah pakai array, dimana arraynya dimulai dari 1, array ke 0 tidak dipakai agar lebih mudah.
Hubungan antar parent dengan anak kanan dan kiri dalam array sangat mudah untuk di cari, dengan x adalah array dari node itu sendiri
•Parent(x) = x / 2
•Left-child(x) = 2 * x
•Right-child(x) = 2 * x + 1
misalnya, node 15, x= 2, parentnya 1, anak kirinya 4, dan anak kanannya 5.
Aplikasi heap yaitu dalam Priority Queue
- Selection Algorithms (finding min/max element, median, kth-largest element, etc).
- Dijkstra’s Algorithm (finding shortest path in graph)
- Prim Algorithm (finding minimum spanning tree)
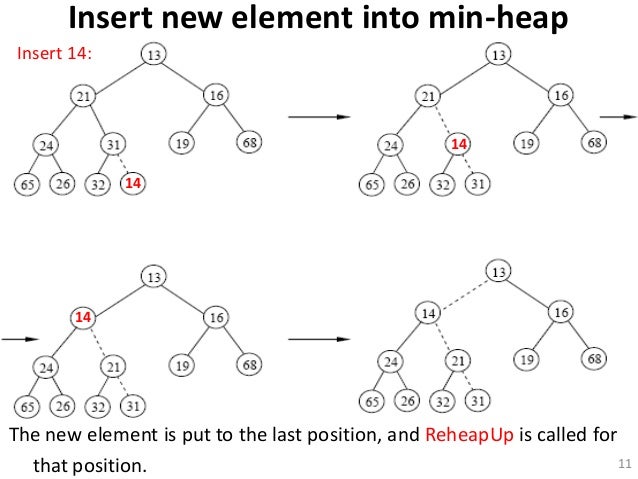
Insert heap
Insert element di node array terakhir, lalu di upheap(fixing heap property).
Upheap
Dibandingkannya angka yang di insert dengan parentnya, klo yg di insert < , maka dituker, begitu terus sampai parentnya yang < dari anaknya atau angka yg diinsert sudah sampai root(ga pnya parent).

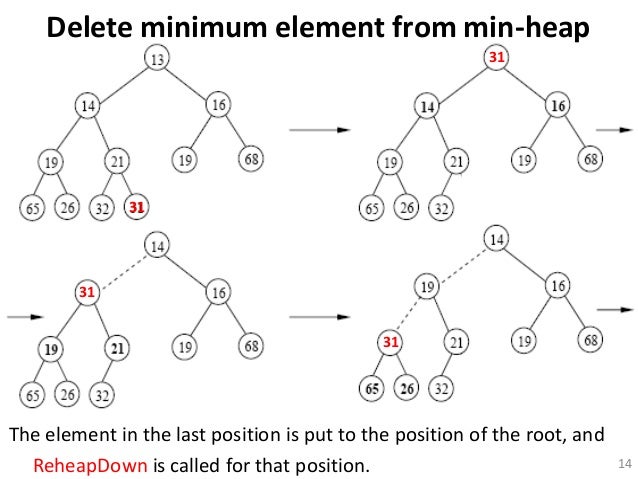
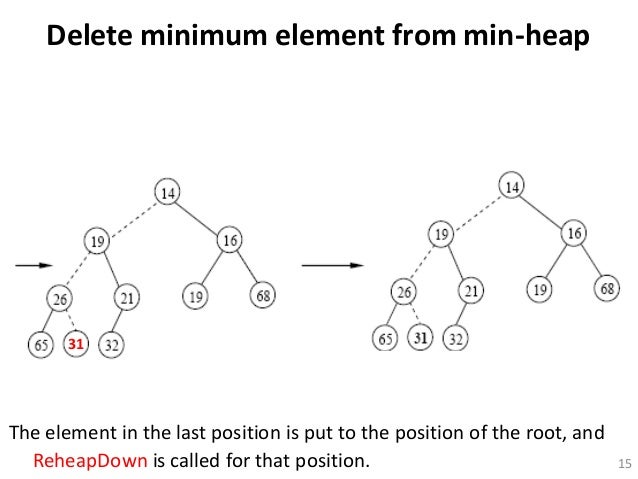
Deletion in Min-heap
Delete hanya bisa dilakukan di angka terkecil(root), lalu root digantikan oleh element array terakhir, lalu mengurangi number element dalam heap, dilakukan downheap(fixing heap property)
Downheap
mengcompare current node(awalnya root dulu) dengan anak kanan dan kiri, lalu swap current node dengan anak paling kecilnya, lalu lanjut downheap yang anaknya. stop downheap saat parentnya > dari kedua anaknya atau sudah sampai di leaf(tidak punya child).


Max-heap
Max-heap bisa untuk Priority Queue (yang lebih besar duluan)
Setiap node > dari anak-anaknya. Node paling besar ada di root. Prinsip Max-heap=Min-heap

Min-Max heap
Gabungan min dan max heap. Agar bisa menemukan angka terkecil dan terbesar bersamaan.
Angka terkecil ada di root, angka terbesar ada di anak kanan/kiri root. Root bisa menjadi angka terbesar kalau nodenya cuma 1(root doang)
Insertion dalam Min-max heap
insert element baru di array paling terakhir, lalu melakukan Upheap .
Upheap
1. Jika new node ada dalam min-level :
- If new node's parent<, maka swap ,lalu upheapmax dari parentnya
- else, upheapmin dari new node
2. Jika new node di max-level :
- If newnode's parent>, maka swap, dan upheapmin dari parent
- else, upheapmax dari new node
Upheapmin
membandingkan current node dengan grand-parentnya. jika current node< parent, maka swap, dan lanjut upheapmin grand-parent node.
Upheapmax
membandingkan current node dengan grand-parentnya. jika current node>parent, maka swap, dan lanjut upheapmax grand-parent node.
Deletion in Min-Max heap
1. Deletion smallest element
- replace root dengan element terakhir.
- kurangi jumlah element heap
- downheapmin dari root
2. Deletion largest element
- replace angka paling besar dengan last element heap
- kurangi jumlah element heap
- downheapmax dari node
Downheapmin
bikin current node jd angka paling kecil dari smua node
- klo m itu grandchildren dari current node. klo grandchildrennya < current node, swap, lalu jika m>parent, swap, trs downheapmin dari m
- klo m itu anak dari current node, dan m<current node, swap
konsep downheapmax=downheapmin
Tries
Tries (prefix tree) adalah ordered tree data structure yang digunakan untuk array associative(biasanya string). Tries mampu mencari kata dalam dictionary hanya dengan prefix dari katanya sendiri.
Tries adalah tree yang setiap vertex menghasilkan 1 kata/prefix. Root dalam tries isinya empty character. Vertex yang jarak dari rootnya k edges , memiliki prefix dengan panjang k.

BTree
B -Tree merupakan data structure yang mempercepat
pengaksesan data. Dimana BST akan selalu balance., krna klo nodenya penuh, dia
bakal bikin root baru, bukan leaf baru. BST memiliki 1
value tiap node, dan memiliki 2 percabangan/anak. Jadi BST bisa disebut
Two-way Tree.
Jadi bisa
disimpulkan dengan M-way tree, dimana M
itu maksimal jumlah anak/cabang dari setiap nodenya. Dan setiap node memiliki M-1 values /key . Setiap node(kecuali root) punya anak minimal
M/2->dibuletin keatas(gayakin). Akar(jika bukan leaf) paling sedikit
memiliki 2 anak/cabang. Node yg bukan leaf, memiliki k anak,punya k-1 keys.
Setiap leaf, ada di level yang sama(paling bwh).
2-3 B-tree àM=3
1.
Jadi, yg bukan leaf, bisa 2 node(punya 1 key, 2
anak->left&middle) atau bisa 3 node(2 key, 3 anak->left,middle,right)
2.
All data are kept in sorted order.
-misalnya, 2 node, menyimpan 1 key yaitu A.
maka data left subtree <A, dan data middle subtree >A
- misalnya ,3 node, meyimpan 2 key, yaitu A
dan B. Maka left subtree<A, middle subtree diantara A&B, right subtree
>B.
Insert:
1.
Misalkan yang mau di insert key.
2.
Mencari peletakan key yang tepat
3.
Jika sudah ditemukan, maka lihat leafnya;
-jika leaf 2 node, maka insert saja keynya
->sehingga leaf menjadi 3 node.
- jika leaf 3 node, maka masukkan. Namun
middle data dari leaf tersebut dipindahkan ke parent, lalu 2 leaf tersebut
dipisah menjadi 2 node masing-masing. Recursive fix parent.
Deletion:
1.
Hrs cari leaf pengganti klo delete key. Jd
delete slalu trjadi di leaf.klo yang di delete bkn leaf, pilih leaf buat
gantiin yg mw diapus, abis itu baru apus leaf yg di bwh.
Jika:
-Leaf nya 3 node, delete aja, maka key nya
jd 2 node
-Leafnya 2 node:
-jika
parentnya 3 node, ambil 1 key drnya. Klo siblingnya 3 node,push 1 node sibling
ke parent(biar parent jd 3 node lg), klo siblingnya 2 node, bikin parent 2
node, dan merge current node with its
sibling
-jika
parentnya 2 node. If siblingnya 3 node, ambil 1 node dr parent dan push 1 node
dari sibling ke parent. Else, merge parent with sibling
2. fix
parent recursively.
B-Tree(order 4&5):
Proses insert sama seperti 2-3Tree.
Delete:
1.
Hrs cari leaf pengganti klo delete key. Jd
delete slalu trjadi di leaf. Misalnya yg mo diapus, nama leafnya p.
2.
Klo p>m/2, apus aja
3.
Klo p=m/2 maka;
-
Siblingnya jd q
-
Klo size q>m/2, rotate value ke p(via parent)
-
Klo q=m/2, merge p&q&1 key dari parent
4.
Fix parent recursively.



Comments
Post a Comment